HARİTA MÜHENDİSLİĞİ BAKIMINDAN ÖNEMLİ GÖRÜLEN HİKMETLER

Doç. Dr. Hüseyin İNCE,
Trakya Üniversitesi, Teknik Bilimler Meslek Yüksekokulu, Sarayiçi/Edirne.
[email protected],

Dr. Öğr. Üyesi Nuri ERDEM
Osmaniye Korkut Ata Üniversitesi, Müh. Fakültesi, Harita Müh. Bölümü.
[email protected],

Varlık yaratılmamıştı ve Allah’tan başka hiçbir şey yoktu[1]. Yüce Allah, zatının tanınmasını ve bilinmesini istedi. İsim ve sıfatlarının tecellisi olarak kâinatı yarattı. Bir hadis-i kutside yüce Allah: “Ben gizli bir hazine idim, bilinmek ve tanınmak istedim, mahlûkatı yarattım.” buyurmuşlardır. Yani yüce Allah kâinatı kendisini tanıtmak için yaratmıştır. Yaratılışın gayesi ve amacı Yaratıcıyı tanımaktır[2].

Yüce Allah Kur’an-ı Kerim'de;

“O Allah yaratıcıdır, her şeyi yoktan yaratandır, her şeye suret ve şekil veren odur. Bütün güzel isim ve sıfatlar ona aittir. Semavat ve arzda bulunan her şey onu över, onu tesbih ve her türlü noksan sıfatlardan tenzih eder. O azizdir, izzet ve azamet sahibidir. Her işi hikmetledir, her yaptığı şey ilim ve hikmetin gereğidir”[3]. Buyurarak bu hususu ifade etmiştir[4].

Kâinatın yaratılışında harita mühendisliği bakımından önemli sayılacak hikmetler; yeryüzünün küre şeklinde yaratılışı, kutup yıldızı, pi sayısı, manyetik kuzey yönü ve yaratılmış bazı canlı varlıklarda görülen fiziki şeklin özelliği olarak ifade edilebilir. Bu çalışmada, burada belirtilen hikmetler detaylı olarak açıklanacaktır.

Yeryüzünün Küre Şeklinde Olmasının Hikmetleri

Harita mühendisliğinde yeryüzünün en genel şekliyle küre şeklinde olmasının faydaları üç şekilde özetlenebilir:

Jeodezik astronomi çalışmalarında,
GPS Tekniği ile konum belirleme çalışmalarında,
Yeryüzünde haritası yapılacak sahanın alan büyüklüğünün 5000 km2’yi aşması halinde yeryüzünün şeklinin küre olarak kabul edilmesinde.

Gök küresi (Şekil 1), tüm gök cisimlerinin sonsuz yarıçaplı bir küre üzerine düşünce olarak izdüşürülmesiyle oluşur. Küre astronomisi, yeryüzünden belirli bir anda göründüğü biçimiyle, gök küresi üzerindeki yıldızların birbirlerine göre konumlarının belirlenmesiyle uğraşır[5].

Bu durumda yıldızlar arasındaki açı cinsinden ifade edilen küresel uzunluklar, küresel açılar ve trigonometrik bağıntılara dayalı küresel üçgen çözümleri anlam kazanır.

Jeodezik amaçlarla yapılan astronomik gözlemler ve ilgili hesaplamalar Jeodezik Astronomi altında ele alınır. Jeodezik astronomiye konu olan başlıca ölçme türleri;

Enlem ve boylam ölçmeleri (Şekil 2).
Zaman ve yıldız konumlarının belirlenmesi.
Azimut belirleme (Şekil 3).
Yeryüzünde cami yapılacak bir yerin ve Kâbe’nin coğrafi koordinatları elde edildikten sonra yapılacak cami veya mescit için kıble azimut açısının hesaplanması ve aplikasyonu.

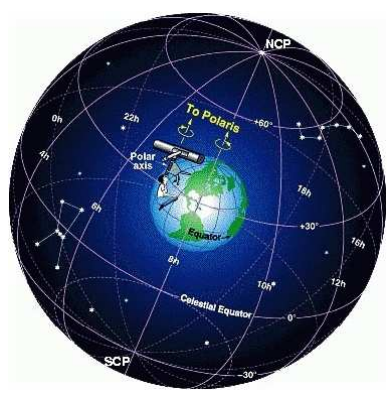
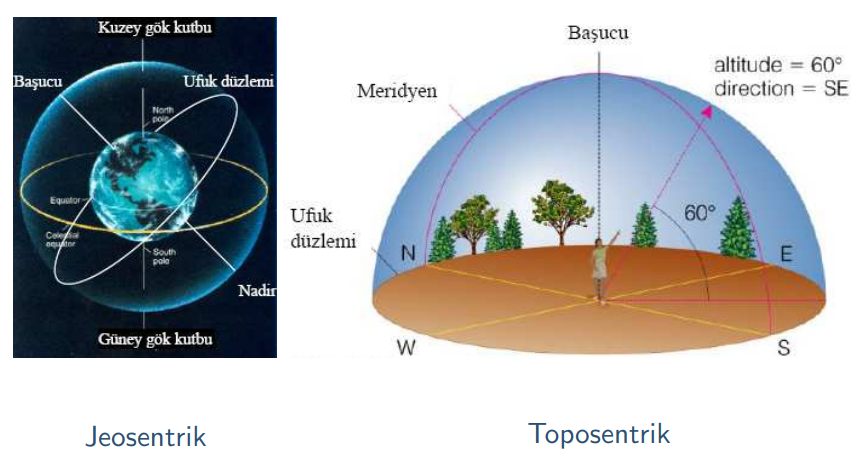
Şekil 1. Gök küresi.

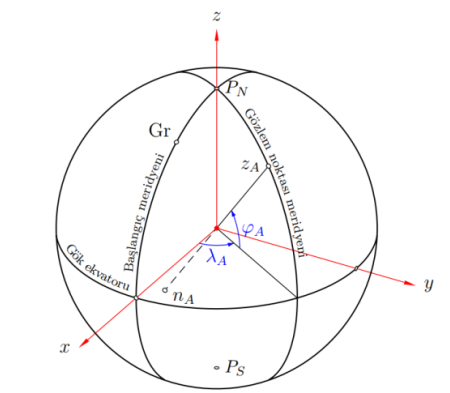
Şekil 2. Enlem ve boylam daireleri.

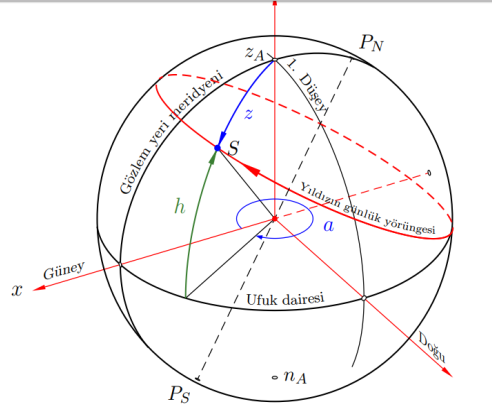
Şekil 3. Azimut açısının belirlenmesi.

Yukarıda belirtilen jeodezik konuların açıklığa kavuşturulması, problemlerin çözümü için yeryüzünün küre olarak kabul edilmesi gerekmektedir. Aksi halde yeryüzünde bir noktanın coğrafi koordinat sisteminde tanımlanması ve buna bağlı olarak yeryüzünde bir noktanın ve Kâbe’nin coğrafi koordinatları (enlem ve boylam değerleri) bilinmediği takdirde bir noktada kıble azimut açısını hesaplanması ve kıble yönünün aplikasyonu mümkün olmaz.

Global Positioning System (GPS) olarak bilinen "Küresel Konumlama Sistemi", 1974' te Amerikan Savunma Bakanlığı tarafından üç boyutlu konum belirleme amacına yönelik geliştirilmiş bir uydu sistemidir. Küresel Konum Belirleme Sistemi (GPS/GNSS), yer konum belirleme sistemlerinin uygulanmasında çıkan sakıncaları ortadan kaldıran, en az 4 uydudan kod‐faz varış zamanının ölçülmesi esasına dayanan üç boyutta yüksek doğrulukta konum ve hız belirlemeyi sağlayan bir sistemdir. Her türlü hava şartlarında sürekli kullanılabilen, sınırsız sayıda kullanıcının yararlanabileceği, doğru zamanın ölçüldüğü dış etkilere karşı güvenilir bir yapıdadır (Şekil 4, 5, 6)[6].

Uydulardan yararlanılarak yapılan GPS ölçmelerinde, elektromanyetik dalgalar kullanılarak uydulardan kullanıcılara veri akışı sağlanmaktadır (Şekil 5). Her GPS uydusu, konum belirleme amaçlı olarak iki temel frekansa sahiptir. GPS alıcısı, dünya üzerindeki yerini belirleyebilmek için uydularla bağlantı kurmak zorundadır (Şekil 5, 6).

Bağlantının gerçekleşebilmesi için alıcının gökyüzünü rahatça görebilmesi gerekir. Günümüzde CORS-TR uygulaması sayesinde tek bir GNSS alıcısı ile konum belirlemek mümkündür (Şekil 6). Uydu ile kullanıcı arasındaki mesafe ölçümü prensibine dayalı olan sistem dünyanın her yerinde hizmet verebilmektedir (Şekil 7).

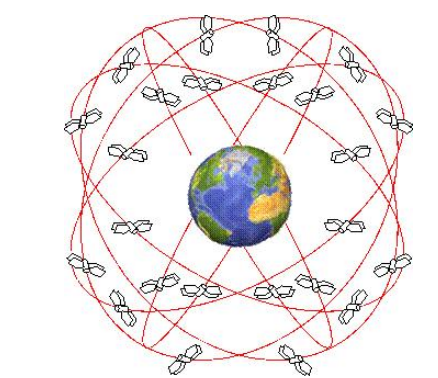
Şekil 4. GPS/GNSS uyduları.

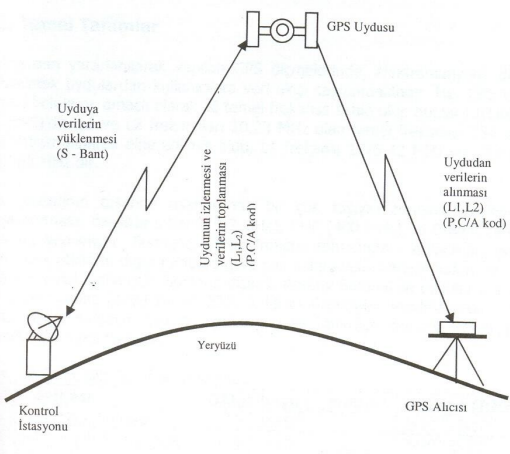
Şekil 5. GPS/GNSS bölümleri ve veri akışı.

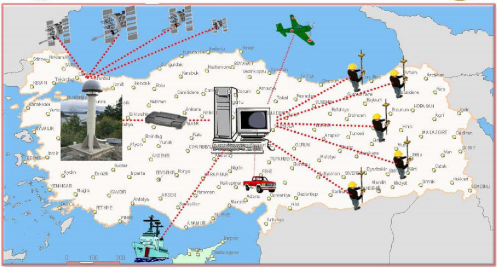
Şekil 6. CORS-TR uygulaması.

Şekil 7. Uydu alıcı arası mesafe ölçümü.

GPS sistemi, World Geodetic System 1984 (WGS84) sistemini kullanır ve yeryüzünde bulunduğunuz noktayı 300 fit (90 M) yüksekliğe kadar kesin bir şekilde bulabilir. GPS uyduları, yer küresinin etrafında uzayda, yeryüzünden 20 000 km. uzaklıkta, bir küresel yörünge üzerinde hareket etmektedir. Yörüngenin şeklinin küre şeklinde olması, yeryüzünde yapılacak haritacılık faaliyetlerinde, uydularla iletişimi kolaylaştırmaktadır. Dünyanın şekli küre olduğu için, uydu yörüngesinin de küre şeklinde olması gerekmektedir.

Yüce Yaratanın yarattığı her şeydeki hikmetler, günümüz teknoloji çağında daha iyi anlaşılmaktadır.

Kutup Yıldızının, Haritacılık Çalışmalarındaki Hikmeti

Kutup Yıldızı, dünyanın ekseni ile hemen hemen aynı doğrultuda olduğundan, diğer gökcisimlerinin aksine gün boyunca yer değiştirmez ve hep kuzeyi gösterir. Bu özelliği sebebiyle, tarih boyunca yön bulma ve seyir amacıyla kullanılmıştır. Bu sebeple, Demirkazık, Kuzey Yıldızı gibi isimlerle adlandırılmıştır (Şekil 8, 9).

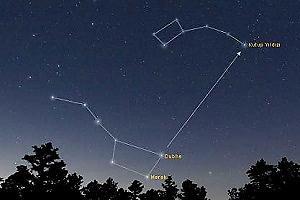
Şekil 8. Kuzey/kutup yıldızı.

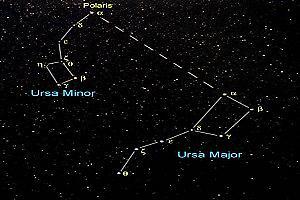
Şekil 9. Kuzey/kutup yıldızı.

Kutup yıldızı, tam kutup noktasının üstünde olması sebebiyle tam olarak kutup noktasını gösterir ve bu sebeple Kutup yıldızı ismiyle anılır. Kutup yıldızı, kutup hizasındaki yerinden bir yıl boyunca çok az bir miktar yer değiştirir. Bu yer değiştirme miktarı, en fazla 44’e kadar, en az ise 30’dur. Kutup yıldızının, en genel konumuyla yer değiştirmemesi ve sürekli olarak aynı yerde kalması sebebiyle, yön bulmak için kullanılan önemli bir yıldız olmuştur. Kutup yıldızı, kuzey yarım kürede ve kuzey kutup noktası üzerinde bulunduğundan, güney yarım küreden kutup yıldızı görünmez[7].

Haritacılık çalışmalarında arazide işaretli iki noktadan geçen bir doğrunun başlangıç kabul edilen noktasında, kutup yıldızından itibaren ölçülen yatay açısı, ilgili doğrunun azimut açısı (semt açısı) olarak ifade edilir. Bir ülkenin veya bir bölgenin ilk tesis harita yapımında orijin kabul edilen noktasında ve oluşturulan nirengi ağının belirlenen noktalarında azimut ölçmeleri yapılır. Nirengi noktalarının koordinat hesabında azimut açısı çok önem arz eden bir faktördür. Gerek ülkemizde gerekse dünya genelinde yapılan haritalarda, harita altlığının üst kısmı kuzeyi, alt kısmı güneyi, atlığın sağ tarafı doğuyu, sol tarafı ise batıyı gösterir.

Yeryüzündeki bir noktanın koordinatlandırılmasında; yeryüzündeki bir noktanın açısal olarak bağlanabileceği tek yıldız kutup yıldızıdır. Yüce yaradanın kutup yıldızını yaratmaktaki en büyük hikmeti, yeryüzünde yön bulmak ve harita yapımında noktaların bağlanacağı sabit bir dayanak olmasıdır.

Pi Sayısının Haritacılık Çalışmalarındaki Hikmeti

Haritacılıkta açı birimi olarak genellikle derece birimi, grad birimi ve çok seyrek olarak radyan birimi kullanılır[8].

Derece sisteminde bir daire 360 eşit parçaya bölünür, bir parçayı merkezden gören açı 1o olarak ifade edilir. Grad biriminde bir daire 400 eşit parçaya bölünür, bir parçayı merkezden gören açı 1g olarak ifade edilir. Derece sistemi 60’lık, grad sistemi ise 100’luk sistem olarak da adlandırılır. Grad sisteminde açının dakika ve saniye birimlerini grad birimine çevirmek ve hesap yapmak çok kolay olduğundan, haritacılıkta kullanılan yatay ve düşey açı ölçmeye yarayan gerek eski aletler ve gerekse yeni aletlerin açı bölüm daireleri grad biriminde bölümlendirilmiştir. Radyan biriminde, bir dairede yarıçap uzunluğundaki yay parçasını dairenin merkezinden gören açı, bir radyan olarak kabul edilir.

Açı birimlerini birbirine dönüştürmek için; αg/200= αo/180= αr/π bağıntısı kullanılır.

Pi sayısının matematik biliminde bir sayının da ötesinde temel bir “sabit” kabul edilmesi, daire ile olan ve hiçbir zaman değişmeyen ilişkisinden kaynaklanır. Pi sayısı, “bir dairenin çevresinin, çapına bölünmesi” ile bulunur. Pi sayısının simgesi, Eski Yunanca çevre manasına gelen “περίμετρον” sözcüğünden gelmektedir ve bu nedenle günümüzde “π” sembolü ile gösterilir. Ludolph sayısı ve Arşimet Sabiti olarak da bilinen Pi sayısı, hakkında belki de en çok spekülasyon yapılan matematik sabitlerinden biridir[9].

Pi sayısının bir dairenin alanının ve çevresinin bulunmasında da gerekli olduğu bilinmektedir. Günümüzde arazide detay ölçümü esnasında bir noktaya ait yatay açı doğrudan ölçülemezse, bu noktanın yakınında, yaklaşık daire yayı üzerinde olacak şekilde yardımcı bir nokta alınır, yardımcı ölçülerle, ölçülecek nokta ile yardımcı noktayı birleştiren yayı gören açı, önce radyan biriminde sonra, yukarıdaki bağıntıdan dönüşüm yapılarak grad biriminde hesaplanır.

Günümüzde açının, radyan biriminde diğer mühendislik dallarında kullanıldığı, bilgisayarda yapılacak hesaplamalarda açının radyan biriminde girilmesi gerektiği bilinmektedir. Pi sayısının önemi, yukarıda belirten açıklamalardan sonra, yüzyılımızda mühendislik projelerinde daha da iyi anlaşılmaktadır.

Manyetik Kuzey Yönünün, Haritacılık Çalışmalarındaki Hikmeti

Manyetik Kuzey Kutbu, Dünya’nın manyetik alanının yayılmaya başladığı noktadır. Gerçek Kuzey Kutbu'na yakın bir konumdadır. Geçmiş yıllardaki bazı teknik çalışmalar neticesinde, herhangi bir pusulanın kuzey ucu Kuzey Kutbu'nu (gerçek kuzeyi) değil, Manyetik Kuzey Kutbu'nu (manyetik kuzeyi) gösterdiği ortaya çıkmıştır (Şekil 10).

Şekil 10. Manyetik kuzeyi gösteren pusula.

Günümüzde manyetik kuzey yönünü gösteren pusula ile yer üstünde ve yeraltında yön tayininde ve konum belirlemede basit olarak bu görevi sağlayan aletler kullanılır (Şekil 11, 12,13).

Yeraltında yapılacak mühendislik projelerinin uygulamasında ise hassas olarak manyetik kuzey yönünü gösteren jiroskop adı verilen aletlerden yararlanılır (Şekil 14). Jiroskop adı verilen, bir noktaya kurulan aletin yöneltme ekseni, yaklaşık olarak manyetik kuzey yönüne getirilerek alet özel bir motor düzeneğiyle çalıştırıldıktan sonra, aletin dürbünü kesin manyetik kuzey yönüne yönelmektedir.

Şekil 11. Askeri pusula.

Şekil 12. Pusula ve açıölçer

Şekil 13. Pusula ve ölçekli cetvel.

Şekil 14. Jiroskop.

Kâinatın yaratılışında yüce yaradan tarafından teşkil edilen manyetik kuzey yönünün, günümüzde yeraltında yapılan büyük mühendislik projelerinde çok gerekli bir faktör olduğu görülmektedir.

Salyangoz Şeklinin Hikmeti

Dünyada yaratılan salyangoz kabuğunun şekli (Şekil 15, Şekil 16), matematikte klotoid olarak tanımlanan eğri şekline büyük benzerlik göstermektedir (Şekil 17). Trafik yollarının projelerinde basit çalışmalarda doğru ve daire yayları, büyük projelerde ise ek olarak geçiş eğrileri de kullanılır. Geçiş eğrileri aliyman ile kurp arasına yerleştirilen eğrilerdir[10].

Günümüzde otoban olarak adlandırılan yüksek hızla gidilen yollarda, aliymanda seyreden bir aracın yatay kurba (viraja) girdiğinde, hızını kesmeden yola devam edebilmesi ve merkezkaç kuvvetinin etkisiyle savrulmasını önlemek için aliyman ile kurp arasına geçiş eğrileri yerleştirilir. Taşıtın direksiyonu geçiş eğrisi üzerinde sabit bir Δє açısal hızı ile döndürüldüğünde, kurba girişte en büyük dönüş acısı elde edilmiş olur[11].

Şekil 15. Salyangoz. Şekil 16. Klotoide benzeyen Salyangoz kabuğu.

Yol projelerinde; yolun aliyman kısmında eğrilik (K) sabit = 0, yolun yatay kurbunda (daire yayında) 1/R şeklinde sabit eğrilik, geçiş eğrilerinde ise değişken bir eğrilik söz konusudur.Klotoid, geçiş eğrisi olarak kullanılan bir eğridir. Denklemi L.R = A2 olup, L geçiş eğrisi uzunluğu ile R kurp yarıçapının çarpımı bir A sayısının karesine eşittir. A=1 alınırsa bu klotoide birim klotoid adı verilir[12].

Klotoid, eğriliği K = 0’dan K = ∞’a giden ve sürekli doğrusal artan bir eğridir. Her defasında ilgili yarıçap ile gelişi güzel eğri uzunluğunun çarpımı sabittir.

L.R = sabit

Bu denklemin sabit terimi ikinci dereceden gösterimle A parametresi şeklinde ifade edilerek bir boyut formülü çıkarılır.

A2 = R.L A=√ (R.L) (1)

     A: Klotoid parametresi [m]
     R: Klotoidin sonundaki yarıçap [m]
     L: Klotoid uzunluğu [m]

Klotoid’de eğrilik (K), uzunlukla lineer değişir. Bu nedenle sürücü direksiyonu değişmeyen açısal hızla döndürebilir.

K = dt/dL =1/R =L/A2 (2)

Klotoidin şekli ve sağladığı faydalar görüldükten sonra, Yüce Yaratanın, salyangozdaki bu eğrileri boşuna yaratmadığı anlaşılmaktadır.

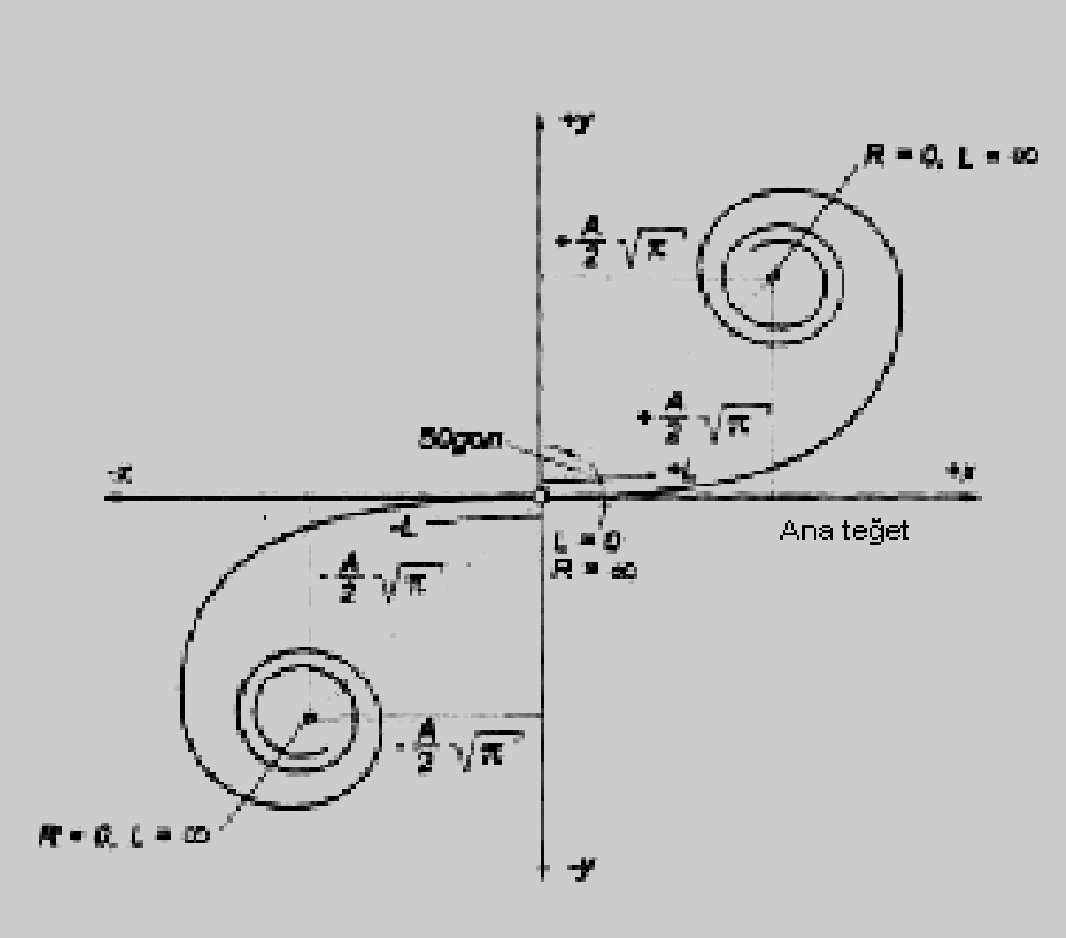
Şekil 17. Koordinat sisteminde klotoid.

Sonuçlar

Kâinatın yaratılışında harita mühendisliği bakımından önemli sayılan hikmetler, yukarıda detaylı olarak belirtilen açıklamalardan sonra aşağıdaki şekilde sıralanabilir:

Yeryüzünün şeklinin en genel şekilde küre olmasının hikmetleri; yeryüzünde bir noktanın coğrafi koordinat sisteminde tanımlanmasını ve buna bağlı olarak yeryüzünde bir noktanın ve Kâbe’nin coğrafi koordinatları (enlem ve boylam değerleri) bilindiği takdirde kıble azimut açısını hesaplanmasını ve kıble yönünün aplikasyonu mümkün hale getirmesidir. Ayıca GPS yöntemiyle konum belirleme çalışmalarında; uydular bir küresel yörünge üzerinde hareket ettiğinden dolayı, yörüngenin şeklinin küre şeklinde olması, uydularla iletişimi kolaylaştırmaktadır.
Kutup yıldızının, haritacılık çalışmalarındaki hikmeti; kutup yıldızının, kuzey kutup noktasında olması ve konumunun sabit durumda olması nedeniyle, yeryüzünde yön bulmak ve harita yapımında noktaların bağlanacağı sabit bir dayanak olmasıdır.
Pi sayısının haritacılık çalışmalarındaki hikmeti; muhtelif mühendislik dallarında bir daire yayını merkezden gören, radyan biriminde ifade edilen açının, derece veya grad birimine dönüştürülmesinde, bu açı birimleri arasındaki ilişkiden yararlanılır. Belirtilen bu ilişki içinde pi sayısı yer almaktadır. Ayrıca günümüzde bilgisayarda yapılacak hesaplamalarda; açının radyan birimi kullanılır.
Manyetik kuzey yönünün, haritacılık çalışmalarındaki hikmeti; manyetik kuzey yönünü gösteren pusula ile yer üstünde ve yeraltında yön tayininde ve konum belirlemede basit olarak bu görevi sağlayan aletlerden, yeraltında yapılacak mühendislik projelerinin uygulamasında, hassas olarak manyetik kuzey yönünü gösteren jiroskop adı verilen aletlerden yararlanılmasıdır.
Salyangozun şeklinin hikmetlerinden birisi de, yol projelerinde geçiş eğrisi olarak kullanılan klotoid eğrisine ilham kaynağı olmasıdır. Klotoidin şekli ve en ideal geçiş eğrisi olarak sağladığı faydalar görüldükten sonra, Yüce Yaratanın, salyangozdaki bu eğrileri boşuna yaratmadığı anlaşılmaktadır.

[1] Buhârî, Megâzî, 67.
[2] https://sorularlaislamiyet.com/kainat-konusunda-en-cok-merak-edilenler, Erişim Tarihi: 12.11.2017.
[3] Haşr Suresi, 24.ayet.
[4] http://kuran.diyanet.gov.tr/tefsir/sure/59-hasr-suresi, Erişim Tarihi: 15.11.2017.
[5] Aksoy, A., (1987). Jeodezik Astronominin Temel Bilgileri (Küresel Astronomi), İTÜ Matbaası, 2. Baskı, İstanbul; Üstün, A. (2006). Jeodezik Astronomi Ders Notları, Selçuk Üniversitesi.
[6] Kahveci, M. ve Yıldız, F., (2005). GPS Konum Belirleme, Nobel Yayınları, Ankara.
[7] Aksoy, A., (1987). Jeodezik Astronominin Temel Bilgileri (Küresel Astronomi), İTÜ Matbaası, 2. Baskı, İstanbul.
[8] Özbenli, E.&Tüdeş, T., (1989). Pratik Jeodezi Ölçme Bilgisi, KTÜ yayını, Trabzon.
[9] http://www.matematiksel.org/pi-sayisi-hakkinda-enteresan-bilgiler/, Erişim Tarihi: 08.11.2017.
[10] Tüdeş, T., (1979). Aplikasyon Özel Ölçmeler, KTÜ Müh. Mim. Fak. Yayını, Trabzon.
[11] Yayla, N., (2002). Karayolu Mühendisliği, İTÜ İnşaat Fakültesi Yayını, İstanbul.
[12] Aydın, Ö., (2000). Mühendislik Ölçmeleri, YTÜ Yayını, İstanbul.